This assignment will involve writing three small Python modules. These modules are similar to the examples from class (population estimation and reading level) in that they prompt the user for input values, perform calculations on those values, and display the results in a message. Your modules should follow the same basic style as the examples from class, with a comment block at the top documenting the purpose of the module, meaningful variable names, and readable I/O messages.
Note: you may work with one other person from this section on the first module. If you choose to do so, you must clearly identify your partner, and it cannot be the same person you worked with on homework 1. The second and third modules must be done independently (with the instructor available for help, of course).
In the past two decades, professional baseball has been revolutionized by the use of statistics to analyze player and team performance. The driving force behind this movement was Bill James, who introduced many of the stats used today (e.g., runs created, win share, range factor). Perhaps his most famous innovation is the Pythagorean Winning Percentage, which predicts the winning percentage of a team based on how many runs they score and how many they allow:
expectedWinPercentage = runsScored2 / (runsScored2 + runsAllowed2)
You are to write a Python module, named lastnameBall (where lastname is your last name). When executed, your module should prompt the user for the number of runs scored and runs allowed for a team, then calculate the expected winning percentage using James' formula. It should display this percentage, along with the projected record for the team over a 162 game season. For example:
Hint: Wins and losses should be rounded to the nearest integer. The built-in round function should prove useful here. For example, round(2.4) evaluates to 2, while round(2.6) evaluates to 3.
Hint: When you display multiple values in a print statement, the values are separated by a space. If you want to print values without intervening spaces, you will need to convert them to strings and then concatenate those strings. For example, print(1, 2) will print 1 2, while print(str(1)+str(2)) will print 12.
Hint: To produce a blank line in the output, simply call print without any inputs: print().
One of the consequences of Einstein's Theory of Relativity is the phenomenon of time dilation. As an observer increases in velocity, perceived time actually slows for that observer (relative to an outside observer). For everyday velocities, e.g., riding in a car or airplane, the effect is negligible. However, if spacecraft are eventually invented whose velocities approach the speed of light, the difference in relative time would be dramatic. For example, at 50% of light speed, it would take 618 years for a ship to reach Betelguese (as observed from earth), but it would only seem like 267.6 years on board the ship. The factor by which relative time is reduced is defined by the following formula:
dilationFactor = (1 - velocityPercent2/10000)0.5
Note that raising a value to the 0.5 power is the same thing as taking the square root of that value.
STEP 1: You are to write a Python module, named lastnameTime (where lastname is your last name). When executed, your module should prompt the user for a distance (in light years) and a velocity (as a percentage of the speed of light), then calculate and print the relative time it would take to reach that distance. For example:
STEP 2: Once you have STEP 1 working, modify your module so that it displays time for a number of different velocities. You should place your statements that calculate and print the relative time inside a for loop, which ranges over a number of velocities. Your list of velocities must include 10%, 25%, 50%, 75%, 90% and 99%. For example:
Hint: To arrange the output in columns, you can insert a tab character (\t) between output values. For example, print(12, "\t", 15) would print the two numbers with a tab stop in between.
Hello, Little Turtles chapter of the online text contains numerous examples of using a turtle to draw patterns on a turtle graphics window. This last part will involve using a turtle to draw your initials using commands such as left, right, forward, up, down and goto.
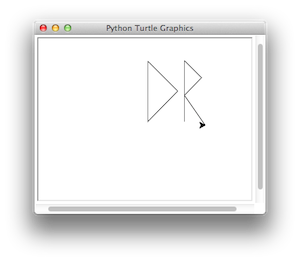
STEP 1: You are to write a Python module, named lastnameTurtle (where lastname is your last name). When executed, your module should draw your initials starting at the center of the turtle graphics window. Your initials should be level (recall that the turtle starts out facing to the right). For example:

STEP 2: Once you have STEP 1 working, modify your module so that it prompts the user for a number, then displays your initials that many times at random positions in the window. You will need to place your statements for drawing the initials inside a for loop, which will repeat the specified number of times. For example, if the user entered 10 at the prompt, the following might be drawn:
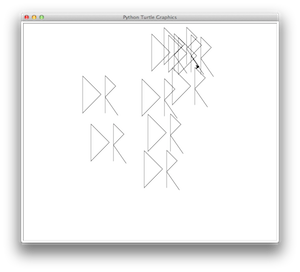
Hint: To generate a random position, you will need to use the goto turtle command and the randint function that is defined in the random module. This means that you will have to add an import random statement at the top of the module, then call the randint function from that module to generate random coordinates. For example, random.randint(-300, 300) will evaluate to a random integer in the range -300 to 300.