In class, we analyzed the add method for the BinaryTree class. Because each recursive call involves counting the number of nodes in each subtree (an O(N) operation) and the number of calls depends upon the height of the tree (which will be roughly log N in a balanced tree), adding an item using this method will be O(N log N). Design a program that will verify this analysis experimentally using techniques similar to HW3. Provide statistics from executions of your program and a coherent argument as to why the statistics support the claim that add is O(N log N).

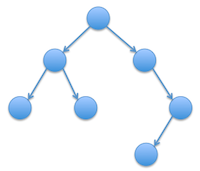
Both of these properties can also be defined using recurrence relations. An empty tree is assumed to have 0 as its height and weight. Otherwise, for nonempty binary tree T:
where size(T) is the number of nodes in tree T. For each of these recurrence relations, provide an inductive proof that the relation does actually hold.
Add methods to the BinaryTree class named height and weight, that calculate and return these tree properties. Initially, you may use the provided size method to test your code. Once it is working, replace the size method with a more efficient version that makes use of a field to keep track of the number of nodes in the tree. That is, the field should be initialized to 0 and incremented/decremented each time an add/remove is executed.
Modify the main method of your BinaryTree class so that it tests each of these methods. Part of your grade will depend upon the thoroughness of your tests.