


In class, we studied the Sudoku class that used recursive backtracking to solve Sudoku puzzles. Sudoku is just one of a family of Japanese grid-based puzzles in which the player must fill the board with values that meet some set of constraints. For Sudoku, the goal is to fill the grid with numbers such that no row, column or subsquare contains duplicate numbers. Other games, such as 3-in-a-row and Range, require the user to fill the grid with colored tiles while meeting additional constraints. BrainBashers.com is a great source of Japanese grid-based puzzles such as these.
For this assignment, you will download the provided Sudoku class and generalize it to create an abstract Puzzle class, which can then be extended to solve many different grid-based puzzles.
Since not all grid-based puzzles utilize numbers or require a square grid, you are to first generalize your copy of the Sudoku class so that it reads in a more generic file format. In the current format, the first line of a Sudoku puzzle file specifies the size of the puzzle (e.g., 9 for a 9x9 grid), followed by a line for each row that specifies its initial contents. In the new format, the first line will specify the values that can be placed in the grid (e.g., 1 2 3 4 5 6 7 8 9), followed by a line specifying the number of columns and rows in the grid (e.g., 9 9), and finally the grid contents. See sudoku1.txt, for example.
You will not only need to modify the Sudoku constructor that reads in the file, but also any method that refers to the grid size or grid values. Instead of a size method, your modified class should have NumRows and numCols methods. Once you have made the required modifications, the provided SudokuDriver class should work as before.
Next, define an abstract class named Puzzle that generalizes your modified Sudoku class. Since the input file format now specifies all the puzzle-specific information, the same constructor should work for all grid-based puzzles. Likewise, numRows, numCols and toString should work independent of the puzzle type, so you should be able to copy-and-paste most of this class. The one method that cannot be generalized is hasConflict, since each puzzle will have its own set of constraints. hasConflict should be an abstract method in the Puzzle class, meaning that it must be implemented by any class that inherits from Puzzle.
Once the abstract Puzzle class is complete, modify your Sudoku class so that it inherits from Puzzle. This new version need only contain two things: (1) a constructor that calls the super constructor and (2) the Sudoku-specific hasConflict method from before. Since your new Sudoku class has the same methods as before, SudokuDriver should still work.
3-in-a-row is another puzzle in which the user must fill a grid, this time with colored tiles. When completed, each row and column must have the same number of black and white tiles, and neither color can appear three or more times consecutively (either horizontally or vertically). For example, the 6x6 3-in-a-row grid on the left has some black and white tiles initially placed (empty spaces are gray). When the puzzle is solved on the right, the empty spaces have been filled so as to meet the constraints.



Define a new class named ThreeInARow that similarly extends the abstract Puzzle class, only this time with a hasConflict method that implements the 3-in-a-row constraints. In addition, rename the SudokuDriver class to PuzzleDriver and modify it so that the user is prompted to specify the puzzle type. For example, it might prompt the user for a letter, where 'S' denotes creating a Sudoku solver and '3' denotes a 3-in-a-row solver. Note that both Sudoku and ThreeInARow objects are Puzzle objects by inheritance, so you can assign a Sudoku object or a ThreeInARow object to a variable of type Puzzle.
The file three.txt has been provided for you. It encodes the 3-in-a-row grid shown above, using the Unicode characters '▣' (▣) for a black tile and '▢' (▢) for a white tile.
Range is yet another grid-based puzzle in which the user places black and white tiles. The initial grid contains some number of white tiles containing numbers, which specify the desired number of adjacent white tiles in that number's row and column. The user must place white and black tiles, with the black tiles serving as walls. In addition, no two black tiles can be placed adjacent to each other (horizontally or vertically). For example, 5x4 puzzle on the left is solved on the right. Note that the tile labeled 4 is adjacent to 4 white tiles: itself, one above, one below, and one to the right. Similarly, all of the other numbers match the adjacent white tiles in their row and column.
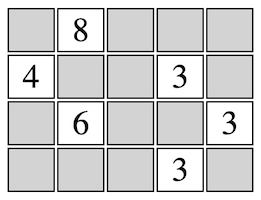


Define a new class named Range that similarly extends the abstract Puzzle class, only this time with a hasConflict method that implements the Range constraints. In addition, add an option to the PuzzleDriver to specify a Range puzzle to be solved.
The file range.txt has been provided for you. It encodes the Range grid shown above, using the same Unicode characters '▣' and '▢'.
If you have the time and inclination, identify a fourth grid-based game from the Japanese-type Puzzles at BrainBashers.com and implement a solver for it.