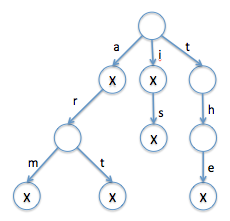
One of the assignments in last semester's CSC 321 course involved implementing a Trie class and using it to store words for a Boggle game. As you may recall, a trie is a tree variant that allows for fast lookup of string values. Unlike a binary tree (where each node has at most two children), a node in a standard trie can have up to 26 children, corresponding to the letters of the alphabet. Within each node, a flag can be set to mark whether the path of letters leading to that node corresponds to a stored string. For example, the diagram below shows a trie that stores 6 words: a, arm, art, i, is, and the. In this diagram, (1) edges are labeled with their corresponding letters, (2) null edges are not shown, and (3) nodes with set flags are marked with an X.

For this assignment, you will extend the Trie class (either your own or my version) so that you can analyze the amount of structure sharing that takes place in the trie.
Trie methodsImplement each of the following recursive (divide & conquer) methods in Trie. Each method must traverse the trie and calculate its result from scratch. You may not add supplemental fields for keeping stats and may not convert the trie structure to another data structure.
/** * Counts the number of nodes in the trie. * @return the number of nodes (including the root node) */ public int numNodes() /** * Counts the number of words that are stored in the trie. * @return the number of words */ public int numWords() /** * Counts the total number of letters in the words that are stored in the trie. * @return the number of letters */ public int numLetters()
Note that the number of letters represented in the trie is not the same thing as the number of nodes. For example, the trie pictured above contains 10 nodes (including the root) and stores 6 words with a total of 13 letters.
The major advantage of tries is that they allow for fast searches. In fact the time required to determine if a word is in the trie is independent of the number of words stored in the tree. It is O(L), where L is the length of the word for which you are searching. For a large dictionary, the speedup can be astounding!
Construct a trie containing all 117,663 words from dictionary.txt. Using your new methods, analyze the amount of structure sharing. How many nodes are required compared with the total number of letters? Would you expect that the Trie representation would require more or less space than a straight ArrayList? Justify your answer, and be sure to submit the driver program you used to generate your data.