CSC 421: Algorithm Design and Analysis
Spring 2017

HW3: Decrease/Divide & Conquer Trees

In CSC 321, we considered implementations of binary trees and (through inheritance) binary search trees. The following classes are simplifications of the versions from last semester: BinaryTree.java, BinarySearchTree.java, and TreeDriver.java. The TreeDriver class generates a binary search tree of a user-specified size, then performs repeated searches and times the result. Using this driver, it is possible to demonstrate that the contains method on a randomly-generated binary search tree is O(log N).

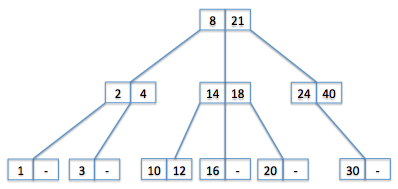
In order to prove the adage that "a log is a log," you are to implement more generic k-ary trees. A k-ary tree stores up to k-1 values in a node, with up to k subtrees. Thus, a binary tree is a 2-ary tree. In a k-ary search tree, the binary search tree property is generalized so that the values in the ith subtree must be greater than or equal to the (i-1)th and ith data values in the node. For example, the diagram below shows a 3-ary search tree of numbers:

Because a k-ary tree divides the values into k subtrees at each level, a randomly generated k-ary search tree will have height proportional to logk N. But while the expected height of k-ary trees decreases as k increases, the amount of work that has to be done to search each node increases. As a result, k-ary trees should exhibit the same O(log N) rate of growth pattern as binary search trees.

To demonstrate this, you are to implement two new classes: KaryTree.java and KarySearchTree.java. These classes will closely parallel the BinaryTree and BinarySearchTree classes, but generalized to k-ary trees. You are required to implement the add, contains, size, and toString methods. In a k-ary tree, adding a value at a given node uses the following rule: if there is space at that node, store it there; if not, randomly select a subtree and add the value to that subtree. Adding to a k-ary search tree modifies this: if there is space at that node, insert it into that node in order; if not, add the value to the appropriate subtree (based on the ordering). The order in which values are listed by toString doesn't matter for a k-ary tree, but for k-ary search trees the values should appear in comparable order. For example, the toString method should return the above 3-ary tree as "[1, 2, 3, 4, 8, 10, 12, 14, 16, 18, 20, 21, 24, 30, 40]". For extra credit, you may implement other methods, such as remove, height, and weight.

Once you have your classes completed and tested, make appropriate modifications to the TreeDriver so that it enables you to time repeated searches on k-ary search trees. Provide data and analysis to answer the following questions:

  1. Do k-ary search trees follow the same rate-of-growth pattern as binary search trees? That is, if you double the size of the tree, does the amount of time it takes to perform a search only go up by a constant amount?
  2. Does the value of k have any impact on the absolute times or the rate-of-growth?