For this assignment, you will modifying and adding to functions that are provided for you in hw5.ss. Download this file and enter your name in the comment at the top.

PART 1: Eliza

One of the most famous/infamous programs from Artificial Intelligence was Joseph Weizenbaum's Eliza. Written in 1966, the Eliza program was intended to demonstrate the superficiality of AI programs at the time. Despite its lack of deep understanding, the program became extremely popular and earned a place in AI history.

The Eliza program is intended to simulate an interview with psychotherapist. The user interacts with the therapist by entering a comment or question, to which the therapist responds with a comment or question of its own. Despite the fact that the program utilizes no language understanding, it is able to often to produce realistic responses due to its pattern-matching capabilities.

A very basic implementation of Eliza can be found in hw5.ss. You begin by evaluating the expression (eliza), and then type in sentences as lists (with all lowercase words and no punctuation). For example,

Make the following modifications to the Eliza rules:

1. The Eliza rules currently include a rule that looks for the word "computer", and responds accordingly. However, this rule will not catch the plural "computers". Add a rule to the database that similarly responds to user input containing "computers".
   
   
2. Add a rule to the Eliza rule database that recognizes the phrase "I miss ___" in the user's input. When this phrase is found anywhere in the user input, Eliza should respond with either "Do you miss other things" or else a response of the form "What do you miss about ___".
   
   
3. Add at least three more rules to the Eliza rule database of your own design. Add a comment next to each new rule to identify it.
   
   

PART 2: Molecular Weight

This association list is also included in the downloaded hw5.ss file. Add the following definitions to the file.

4. Define a function named atomic-number that takes one input, the symbol for an element, and returns the atomic number (i.e., its position in the table) of that element. For example, (atomic-number 'H) should evaluate to 1 while (atomic-number 'O) should evaluate to 8.
   
   
5. Define a function named atomic-weight that takes one input, the symbol for an element, and returns the atomic weight of that element. For example, (atomic-weight 'H) should evaluate to 1.008 while (atomic-weight 'O) should evaluate to 15.9994.
   
   
6. Define a function named molecular-weight1 that takes one input, a list of element symbols, and returns the molecular weight (i.e., the sum of all of the atomic weights) for that list. For example, (molecular-weight1 '(Na Cl)) should evaluate to 58.4428 while (molecular-weight1 '(H H O)) should evaluate to 18.0154.
   
   
7. When writing formulas for molecules in which an element appears multiple times, scientists use subscripts to denote repetition. For example, the formula for water is written H₂O instead of HHO. Copy your molecular-weight1, rename it molecular-weight2, and modify it to handle lists in which an element may be followed by a number. For example, (molecular-weight2 '(H 2 O)) should evaluate to 18.0154.
   
   
8. Complex formulas can contain nested sub-formulas. For example, the formula for isopropyl alcohol is (CH₃)₂CHOH. Copy your molecular-weight2, rename it molecular-weight3, and modify it to handle nested lists. For example, (molecular-weight3 '((C H 3) 2 C H O H)) should evaluate to 60.0964.
   
   

PART 3: Binary Trees

In class, we discussed how structured lists could be used to represent binary trees. For example, the following binary tree is represented by the list to the right:

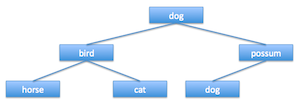
(define ANIMALS '(dog (bird (horse () ()) (cat () ())) (possum (dog () ()) ())))

Several utility functions (empty-tree?, root, left-subtree, and right-subtree) are provided for you in hw5.ss). Add the following functions for manipulating binary trees.

9. Define a function named height that takes one input, a list representing a binary tree, and returns the height (i.e., maximum root-to-leaf path length) in the tree. For example, given the ANIMALS structure above, (height ANIMALS) should evaluate to 3.
   
   
10. Define a function named num-occur that takes two inputs, a list representing a binary tree and a value, and returns the number of occurrences of the value in that tree. For example, given the ANIMALS structure above, (num-occur ANIMALS 'dog) should evaluate to 2.
    
    
11. Define a function named contains? that takes two inputs, a list representing a binary tree and a value, and returns #t if the list contains the value (otherwise #f). For example, given the ANIMALS structure above, (contains? ANIMALS 'emu) should evaluate to #f while (contains? ANIMALS 'cat) should evaluate to #t.
    
    

PART 4: OOP in Scheme

In class, we discussed how first-class functions and closures could support the equivalent of classes, with private data and methods. The following function models a die object, where the number of sides is specified when creating the die.

For example:

12. Modify the code so that there is an additional "method" named num-rolls, which returns the number of times that die object has been rolled. Note: this will involve using non-functional features of Scheme, which is allowable in this instance since those features are hidden inside the object. In particular, you should add a variable definition inside the Die function, initialized to 0. When the roll "method" is called, you will need to update that field (using set!). Also, you should add a num-rolls "method" to enable the user to access the number of times the die has been rolled. For example: > (define d6 (Die 6)) > (d6 'roll) 3 > (d6 'roll) 4 > (d6 'num-rolls) 2